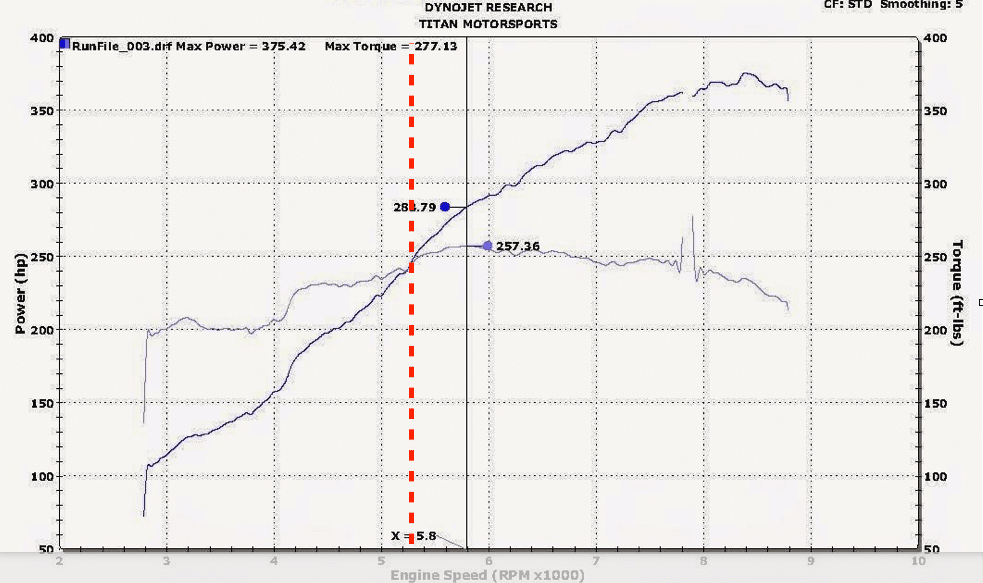
HP and Torque
Horsepower and Torque
by Art Meltzer
It is common knowledge that horsepower and torque are related. Some readers may be aware of what I like to call “the equation” horsepower = torque*rpm/5252. The derivation of “the equation” is beyond the scope of this article however if the reader is interested contact me by email and I will send it to you. My guess is that few of us have insight as to how to apply the equation to the performance of our cars.
A common misconception is “horsepower determines how fast the car will be going when it hits a wall and torque determines how far your car will push the wall”. The initial half of this statement is accurate and the latter half is not. To begin my discussion, I would like to introduce the concepts of torque, work and power.
For units lets use our pounds for force, feet for distance, and minutes for time. Torque (T) is defined as a twisting force applied at a distance. To quantify torque one simply multiplies the force applied (F) times the distance (d) from the application of the force to the object undergoing torque so that T=F*d.
Work (W) is defined as a force F applied to an object causing it to move a distance d. Or W=F*d. For example, if a 10-pound object is removed 60 feet than the amount of work is given by W=60ft*10lbs = 60ft-lbs.
Power (P) is work divided by the time necessary to perform the work. If the 60 foot-pounds of work in the example above is performed in 1minute P=60ft-lbs/min. If the work is performed in 1 hour then P=60ft-lbs/60min = 1ft-lb/min.
In the beginning of the 18th century horses were commonplace and everyone was aware of the power of a horse. James Watt (whose name is immortalized on every lightbulb) determined that the average horse could pull 33,000 pounds 1 foot in 1 minute. Using this he established that one horsepower equals 33,000 foot-pounds per minute of power. Ironically, in the 21st century no one is familiar with the power of a horse but the concept of horsepower is forever embedded in our lexicon.
A gasoline engine is a device that converts the chemical energy stored in gasoline to the mechanical energy of a rotating shaft. Power and torque are two metrics that portray the performance of the engine. That power and torque describe the same phenomenon – engine performance – indicates that power and torque are equivalent concepts. This equivalence can be appreciated by noting that if you measure engine torque on a dynamometer you can use “the equation” to reconstruct HP and vice-versa. Being equivalent concepts, it cannot be said that horsepower means one thing and torque means something else.
As an analogy, consider the purchase of a new Porsche. Currently the German mark is worth $0.57 American. That the number of dollars differs from the number of marks necessary to pay for the car does not mean there is a cost difference in buying the car with marks versus dollars. It means that marks and dollars perform differently as a metric of value but when one takes into account the relationship of the mark and the dollar their purchasing power is equivalent.
One interpretation of “the equation” is that it allows us to separate power into torque (twisting force) and rpm. Torque delivered to the drive wheels is responsible for acceleration.
When accelerating, your engine will cycle in each gear from 4000 rpm-9000 rpm while your wheel speed is constantly increasing. Assuming that there is no loss of energy throughout the drive train the power attained at the crankshaft will be the same as the power delivered to the wheels. “The equation” tells us that the only way this can happen (keeping the power at the rear wheels equal to the power at the crankshaft) is for the torque at the rear wheels to diminish as the rear wheel rpm increases. The loss of torque at the rear wheels at high speed is a major factor explaining why a car’s rate of acceleration decreases as its speed increases.
“The equation” can also give insight into why the torque/horsepower graph has its characteristic appearance. If we divide both sides of “the equation” by torque it looks like:
HP/T = rpm/5252
Consider the case when the rpm is less than 5252. In this case rpm/5252 is a fraction less than 1 so HP/T must be a fraction less than 1. The only way that happens is if horsepower is less than torque. So, the horsepower graph is always below the torque graph when the rpm < 5252.
In a similar fashion if the rpm is greater than 5252, then horsepower > torque and the horsepower graph is always above the torque graph when the rpm > 5252. Lastly, when rpm equals 5252 the curves cross and horsepower equals torque.
Hopefully, this discussion will help to demystify the horsepower/torque relationship.